
Understanding armed conflicts
The new model has already produced interesting results for a simple case–an armed conflict between a governmental group and a rebel group [1]. The model indicates that an eradication of the rebel group cannot always be guaranteed, but that, instead, stalemates arise that can be stationary or periodic. Secondly, the model shows how outcomes are contingent on initial conditions. Lastly, when a conflict is trapped in a periodic stalemate, the model also allows the groups involved to determine when stepping up their efforts would have maximum effect.
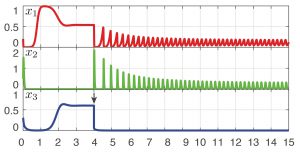
Example of dynamics that may result in a simple model of armed conflict among three groups. One group has the military characteristics and recruitment policies of a governmental army (red), while the other two groups are typical of rebels (green and blue). Over time (horizontal axis), the abundance of different fighters involved in this conflict (vertical axes) changes. At the time indicated by the black arrow, one of the rebel groups (blue) is attacked and eradicated, leading to a resurgence of the other rebel group (green) and its subsequent periodic stalemate with the governmental army (red).
It is generally believed that the outcome of complex conflicts involving rebels and governmental groups cannot be predicted, because data are generally too scarce and unreliable. The results obtained with the new model show that the truth may be even less convenient, as the dynamics among the fighting groups can be extremely sensitive to initial conditions and parameter values [1]. This suggests that the outcome of a conflict may be practically unpredictable, even if very rich data sets were available. This finding, which is common to many complex adaptive systems, challenges the enthusiasm toward data-driven decision making.
According to the researchers, the results obtained so far have proven to be robust. The same results are recovered in a simplified model in which governmental groups are assumed to be purely defensive (i.e., their recruitment depends only on sustained injuries), while rebel groups are supposed to be purely fanatic (i.e., their recruitment depends only on inflicted injuries).
Further research is needed to address important open questions. Some of these are more academic in nature, such as whether armed conflicts exhibit deterministic chaos, peak-to-peak dynamics, and chaotic intermittence, while others are of greater relevance to decision makers, for example, how the models can describe the effects of temporary coalitions or of changes in power and intelligence. Answering these questions requires combining a deep knowledge of case studies with expertise in the theory of nonlinear dynamical systems.
References
[1] Rinaldi S & Della Rossa F (2018). Conflicts among N armed groups: Scenarios from a new descriptive model. Nonlinear Dynamics: 92: 3-12.
Collaborators
- Polytechnic University of Milan, Italy




You must be logged in to post a comment.